HEURISTICA
Admisible
Es una heurística usada para estimar el costo para llegar a
la solución u objetivo. Siempre que el costo estimado sea menor o igual que el
costo mínimo de alcanzar la solución, es una heurística admisible.
H(n) < H*(n)
Donde:
- · H(n)= Costo estimado
- · H*(n)= Costo verdadedo para llegar a la solución
Usa un el algoritmo de heurística para encontrar la mejor estimación
del problema inicial a el problema final donde desea llegar. Generalmente, esta
heurística trabaja con problemas que se asemejan al problema inicial, pero
utiliza menos restricciones.
Monótona
En esta heurística la búsqueda es admisible en todas partes,
la búsqueda es monótona si cumple dos condiciones:
- Para los estados de n(i) y n(j) se ejecuta que:
H(n(i)) – h(n(j)) < costo(n(j),
n(i))
Donde
·
n(j) son todos los sucesores de n(i)
·
costo (n(j), n(i)) es el costo actual, en los movimientos,
para generar los sucesores de n(i)
Heurísticas consistentes
Una heurística es consistente si para cada
nodo (n) y todos sus sucesores (n’) son generados por cualquier acción externa
(A) y el costo estimado de alcanzar el nodo resultado desde el nodo principal,
no es mayor que el costo de obtener los sucesores de n, mas el costo estimado
de obtener el objetivo desde los nodos sucesores
h(n) <
c(n, A, n’) + h(n’)
Las heurísticas consistentes son admisibles,
pero no todas las heurísticas admisibles con consistentes.
Heurísticas más
informadas
Esta heurística permite comparar diferentes heurísticas entre
sí, evalúa cuál de ellas es más informada y determina cuál de ellas es más óptima
para encontrar la mejor solución posible. Es decir, si una búsqueda heurística es
más informada que otra, al hacer uso en
A*, se expandirán menos nodos durante la búsqueda porque lo hará por
profundidad, y habrá nodos sucesores del problema inicial que no tendrá en
cuenta.
Ejemplo de Heuristica:
Aplicaremos la heurística A* para el problema
de los sapos y las ranas teniendo en cuenta que:
- · f(n)= g(n) + h(n) y
- · g(n)=1, siempre que un nodo genere sucesores
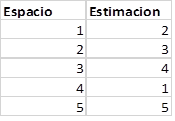
- · la siguiente tabla:
Aplicando el algoritmo,
la prueba de escritorio quedaría:
y el grafo:
Para los lectores
interesados:



No hay comentarios.:
Publicar un comentario